The following are the same as the YouTube page, but with different formats/resolutions.

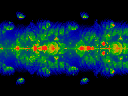
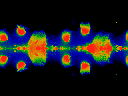
Note that the movies are essentially symmetric about omega=0.5. The four movies above differ only in length, choice of colormap, and length of iteration (the long movies were iterated more, and thus have better resolution).
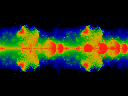
 Click here for a short movie (1.23 MBytes) or
here for a long
move (5.25 MBytes) showing Im omega held constant at 0.1.
Note that ReK runs from -0.2 to 0.2, left to right.
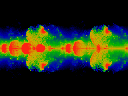
Click here for a short movie (1.23 MBytes) or
here for a long
move (5.25 MBytes) showing Im omega held constant at 0.1.
Note that ReK runs from -0.2 to 0.2, left to right.
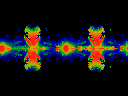
 Click here for a short movie (460K)
showing Im omega held constant at 0.5.
Note that ReK runs from -0.2 to 0.2, left to right.
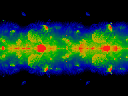
Click here for a short movie (460K)
showing Im omega held constant at 0.5.
Note that ReK runs from -0.2 to 0.2, left to right.
 This (684K) and
this (852K, different colormap)
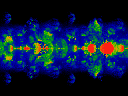
show ReK along x-axis, (running -1 to +1), ReOmega
along vertical axis, and ImK as time, running from 0.0 to 1.0.
Note that there is no periodicity here. ImOmega was held at 0.
Note that the very first frame of teh movie has ImK equal to
0.004. Note that this web site has numerous pictures with
ImK equal to zero -- turned on thier side. Note how even a
slight disturbance (a very small ImK) has all but wiped out
the Arnold's tongues with non-zero winding number.
This (684K) and
this (852K, different colormap)
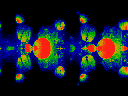
show ReK along x-axis, (running -1 to +1), ReOmega
along vertical axis, and ImK as time, running from 0.0 to 1.0.
Note that there is no periodicity here. ImOmega was held at 0.
Note that the very first frame of teh movie has ImK equal to
0.004. Note that this web site has numerous pictures with
ImK equal to zero -- turned on thier side. Note how even a
slight disturbance (a very small ImK) has all but wiped out
the Arnold's tongues with non-zero winding number.
The following are the same as the YouTube page, but with different formats/resolutions.





















Circle Movies
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.