M-Set Derivatives

One way of coloring the inside of the M-set is to work with the the various derivatives that describe the 'flow' of Z_n. These images are all based on the computation of the derivative of Z_n with respect to c. The expression for this is simple: Z'_n+1 = dZ_n+1/dc = 2 * Z_n * Z'_n + 1, which must be iterated. Note that this derivative can be though of as a vector: it has a real component and an imaginary component. Thus, we can take its curl or divergence as well as it's absolute value.

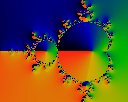
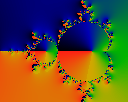
Because Z'_n has a high 'rotation', it is handier to deal with the normalized vector P_n = Z'_n/Z_n Here we graph the phase phi=arctan (Re P_n / Im P_n). Note that not all buds are alike: the interior of some buds see a full rotation of the phase by 360 degrees; others do not.

Very curiously, this seems to depend on the factorization of the loop termination count. When the loop termination count is prime, none of the buds rotate; when it is a product of many small (repeated) factors, most buds rotate. For example, in this image, most buds rotate because iteration was stopped at 1260=4*9*5*7,

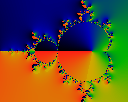
whereas this image stopped at 1259 (which is a prime number) and none of the buds rotate.

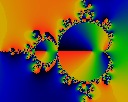
The phase of the second normalized derivative Q_n = Z''_n/Z_n where Z''_n+1 = 2 * (Z_n * Z''_n + Z'²_n)

Modulus of second derivative.

Iterated to a high order (N=4153) before stopping.

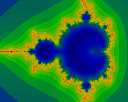
Same image as above, but iterated to only N=19. Note the presence of 'zeros' (black dots) on the interior, which are missing from the high-iteration image.

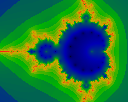
As above, but iterated to N=18. Note that this image contains one less black dot on the belt.

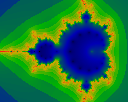
Iterated to N=17. Notice how the images generated with prime N are subtly different than those with composite iteration counts.

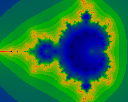
Iterated to N=16. Note that 18 is divisible by 3, while 16 is not: thus the large bud has a green dot in the middle, but the next-smaller one doesn't (unlike the N=18 case).

The second derivative is handy for exhibiting another phenomenon that is hinted at elsewhere in this page, but otherwise difficult to exhibit. This image is created quite artificially: the interior color is recorded only if the modulus of Q_n = Z''_n/Z_n is less than one for some n. In other words, we record the color only if Q_n is near a zero. Thus we see a simultaneous depiction of the zero's of the various Q_n for various n. These seem to go to a hyperbolic-like limit-circle.

In this image, black is zero, moving through blue, green, yellow to a red of 1.0.

Note the Moire patterning make it difficult to discern where the actual limit is. To eliminate this, this image was iterated only to N=50, and so we can see the limit-circle at 50 dots.

The 'distance estimator' is the inverse infinitesimal flow of the iteration number. It gets this name because it provides a rough estimate of how far away an exterior point is from the boundary of the M-Set. The smooth (real-valued) iteration count is given by mu = n+1-log(log(|z|))/log2, as demonstrated in the Escape Theory Room (which is, in turn, the logarithm of the Douady-Hubbard potential). Taking the derivative of mu w.r.t. c we get dmu/dc = d|z|/dc / (|zl log |z| log 2). The 'distance estimator' is one over this quantity.

This first picture shows the iteration to n=9. (We've dropped the factor of log 2).

Iterate to n=19.

Iterate to n=49.

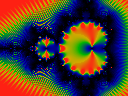
Iterate to n=2520=8*9*5*7 a product of small primes. Oddly, the n=2 bulb is unlit, but n=3 and so on light up.

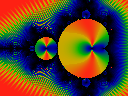
Iterate to n=2519 which is a prime number. Oddly, the n=2 bud lights up, the none of the other buds do. Thus, the counting rules here seem to be a bit different than one might expect ...

Don't confuse the absolute value of the derivative with the derivative of the absolute value.

This image shows |z| / |z'|.

This image shows |z| / |z|'.

M-Set Derivatives by Linas Vepstas is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.