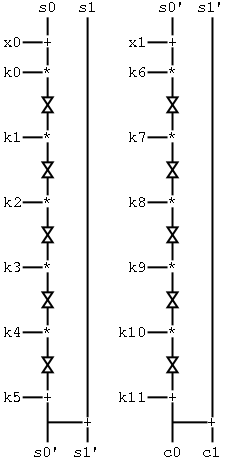
Figure 1: The MultiSwap algorithm
26 October 2001: Add author David Wagner.
25 October 2001
Nikita Borisov, Monica Chew, Rob Johnson, and David Wagner
UC Berkeley
An anonymous security researcher working under the pseudonym "Beale Screamer"
reverse engineered the Microsoft Digital Rights Management subsystem and,
by October 18th, the results
were available on cryptome.org. As part of the reverse engineering
effort Screamer found an unpublished block cipher, which he dubbed MultiSwap,
being used as part of DRM. Screamer did not need to break the MultiSwap
cipher to break DRM, but we thought it would be a fun excercise, and summarize
the results of our investigation below. The attacks described here
show weaknesses in the MultiSwap encryption scheme, and could potentially
contribute to an attack on DRM. However, the attack on DRM described
by Beale Screamer would be much more practical, so we feel that these weaknesses
in MultiSwap do not pose a significant threat to DRM at this time.
We present these results to further the science of computer security, not
to promote rampant copying of copyrighted music.
The Multswap algorithm takes a 64-bit block consisting of two 32-bit numbers
x0 and x1 and encrypts them using the subkeys k0,...,k11 as diagramed
below.

All values are 32-bit, and * and + are normal multiplication and addition
mod 2^32. The
![]() symbols represent swapping the two 16-bit halves of a 32-bit value. When
used in a chained mode of operation, s0 and s1 are the inputs from the previous
block. Otherwise they are 0. Note that the diagram is split into
two stages, and the output from the first half, s0' and s1', is fed into
the second half. So if s0=s1=0, then the input is x0 and x1, and the
output is c0 and c1. Observe also that k0,...,k4,k6,...,k10 must all
be odd if the cipher is to be invertible. Thus the cipher has a 2*32
+ 10*31 = 374-bit key.
symbols represent swapping the two 16-bit halves of a 32-bit value. When
used in a chained mode of operation, s0 and s1 are the inputs from the previous
block. Otherwise they are 0. Note that the diagram is split into
two stages, and the output from the first half, s0' and s1', is fed into
the second half. So if s0=s1=0, then the input is x0 and x1, and the
output is c0 and c1. Observe also that k0,...,k4,k6,...,k10 must all
be odd if the cipher is to be invertible. Thus the cipher has a 2*32
+ 10*31 = 374-bit key.
Consider the algorithm operating on input (0,x1). Since s0=s1=0, it's
not hard to see that s0'=s1'=k5. After the second half, regardless
of the input x1, the output will satisfy c1=c0+k5. Thus one can derive
k5=c1-c0 with one chosen-plaintext message of the form (0,x1).
Given k5, k11 can be recovered with one additional message. Observe
that with input (0,-k5), it will still be the case that s0'=s1'=k5. In
the second half, though, adding x1=-k5 to s0' will yield another 0, which
will propogate through the multiplications and swaps as before. Thus
the output will be c0=k11 and c1=k5+k11.
So k5 and k11 can be exposed with a 2-message adaptive chosen-plaintext
attack.
We first present a chosen-plaintext attack, and then describe how to convert
this to a known-plaintext attack. We will present the attack assuming
that s0=s1=0, but it also works when they are non-zero but known: just use
x0=-s0 instead of x0=0.
The chosen-plaintext attack makes use of the keys k5 and k11 recovered above.
With these keys, one can control the input to the second half of the
encryption. For example, to force the value multiplied by k6 to be
w, simply query the encryption oracle with plaintext (0,w-k5). As for
the output, since k11 is known, given c0 one can partially decrypt to find
the intermediate value computed immediately after the multiplication by k10.
This reduces the problem to the following system for which the input,
w, can be controlled and the output, v, can be observed. The goal is
to recover k6,...,k10.
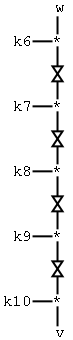
For the rest of this section, "input" and "output" will refer to the input
and output of the above cipher fragment, not the cipher as a whole. As
mentioned above, this is fine since one can perfectly control and observer
these inputs and outputs.
The attack uses differential cryptanalysis. The differential is not
an additive or xor-differential, it is a multiplicative differential.
Suppose the above fragment is given inputs w and 2w. Then clearly
this differential is preserved across multiplication by k6. But when
is it preserved by swapping the two halves of k6*w and k6*2w? In
other words, for arbitrary z, when is
Recall there are two stages to the attack: recover k5 and k11, and recover
the rest of the key. The attack on k5 and k11 can be converted to a
known-plaintext attack as follows. Referring to Figures 1 and 2, observe
that w=c1-c0+x1. With probability 2^-32, this value is 0, and that
situation can be detected. When this happens, c0=k11. So a set
of 2^32 known-plaintexts should suffice to recover k11. Similarly,
s0'=c1-c0-s1. Out of a set of 2^32 known-plaintexts, on average one
plaintext should satisfy x0+s0=0, in which case s0'=k5. Since these
two events are roughly independent, an attacker should be able to recover
k5 and k11 with 2^32 known-plaintexts.
One can also convert the second stage of the attack to use known-plaintexts.
We first have to see that the inputs and outputs of the two halves
of the cipher can be isolated. So suppose an attacker knows k5 and
k11. First observe that c1 = c0 + s0'. So the input to Figure
2 can be computed as w=c1 - c0 + x1. Since he knows k11, an attacker
can also obviously compute the output, v, of the fragment in Figure
2. For the first half of the cipher, the input is x0 (or x0 + s0, which
is known, if used in a chaining mode). The output (immediately after
multiplication by k4) is
![]() (c0-c1-k5).
(c0-c1-k5).
All that's left is to figure out the number of messages one needs to capture
before expecting to have 8192 pairs (w,2w) for the second round and 8192
pairs (w,2w) for the first round. With 2^22.5 known-plaintexts, we
get 2^44 pairs, and the probability that any one of these pairs is of the
form (w,2w) is 1/2^31. Hence we expect to have 2^13 such pairs.
Experiments confirm this estimate. Thus with 2^22.5 known plaintexts,
we expect that the 2^22.5 inputs to the second round will contain about 2^13
pairs, enough to recover k6,...,k10. But these same messages yield
2^22.5 inputs to the first round, which should also contain 2^13 pairs.
Since these events are independent, one should be able to break the
system with 2^22.5 known plaintexts. Detecting the pairs in a set of
known plaintexts is easy if the pairs are stored in a hash-table, so the
work factor is just 2^25, as above.
The known-plaintext attack described above requires 2^32 texts, which seems
like a waste since those texts are only required to recover k5 and k11. By
performing both halves of the attack simultaneously, one can get by with
just 2^22.5 known-plaintexts.
Recall that, even without knowledge of k5 and k11, we can derive the input
to the cipher fragment in Figure 2 via w=c1-c0+x1. If we extend our
differential through the additional swap immediately preceding the addition
of k11, we get a differential (w,2w) -> (v,2v) -> (v+k11,2v+k11) with
probability 1/2^10. Given such a right pair with outputs c0 and c0',
we can compute k11=c0'-2*c0.
So collect 2^22.5 known-plaintexts, and collect from them 2^13 pairs whose
input to Figure 2 is (w,2w). Each such pair suggest a candidate for
k11=c0'-2*c0. The right value of k11 will be suggested once for each
right pair, or 2^13/2^10=8 times. Wrong pairs will suggest a random
value for k11, and so no other value for k11 should be suggested more than
once or twice.
With k11, one can use the previously described attack to recover k6,...,k10.
This attack can then be repeated for k5, and then for k0,...,k4. The
total work factor is about the same as for the previous attacks. The
storage is also quite small, since we don't have to keep a counter for every
possible value of k11, only the ones suggested by a pair. Since we
use only about 2^13 pairs, the storage requirement is about 2^16 bytes.
We have seen that MultiSwap can be broken with a 2^14 chosen-plaintext attack or a 2^22.5 known-plaintext attack, requiring 2^25 work. We believe this shows that MultiSwap is not safe for any use.