Throughts about the MEG principle ( Part 2 )
By Cyril Smith
created on 11-12-00 - JLN Labs - last update on 11-12-00
| Subject : | MEG Theory and thoughts |
| Date : | 12/11/00 11:28:51 Paris, Madrid |
| From: cyrilsmith@camelot64.fsnet.co.uk (Cyril Smith) | |
Hi All,

Cross Flux MEG. I can't see how cross flux
will work with the exotic nanoperm and metglas materials.
In my simple mind these get their terrific BH characteristics
because they are highly anisotropic, the atomic dipoles are all
aligned in the one direction. Thus they would have no
useful BH characteristic in the cross flux direction, they would
simply look like air. There is no internal mechanism for
cross flux control. Statements like Fred has turned up
"when a material is saturated in one direction it is not
saturated in other orthogonal directions" are true only for
isotropic materials. Remember the atomic magnetic dipoles
are fixed in the crystal lattice, they do not wiggle about.
They can and do flip polarity and it is this feature which
accounts for permeability. Imagine say 360 co-located
dipoles each one aligned 1 degree different to its neighbour.
We have a net dipole moment of zero. Now apply a
slowly increasing magnetising force along say the 0 degree axis.
First the 180 degree dipole will switch, then the 179 and 181
degree ones, then the 178 and 182 ones and so on. You will
see that the net magnetisation gradually increases until
saturation is reached where there are no more dipoles available.
Plot magnetisation*munought against magnetising force and you
have B v. H, in the chosen 0 degree direction.
There will be no magnetisation in the 90 degree direction.
Now apply a slowly increasing magnetising force in this new
direction, keeping the original 0 degree H force present.
Again you will see dipoles switching direction to give 90 degree
magnetisation, but some of these were contributing to the 0
degree magnetisation, so this value will fall. Thus you can
only get the 90 degree magnetisation at the expense of 0 degree
magnetisation. This is the cross flux control mechanism.
If all the dipoles are fixed in the one alignment there is no
cross flux control available. GO steel will not be highly
anisotropic, so here there will be some cross flux control.
Now to the non cross flux MEG. Something Dave D said
about flux lines leaving the core rang some bells. It
strikes me that flux lines can and must leave the core, even a
complete magnetic circuit like a ring core. In the MEG the
flux lines from the magnet do so. And it is obvious to me
that if you wound two identical coils on opposite limbs of a ring
core, passed current through these in cancelling mode, you would
have flux lines leaving the core. This would simply be two
banana shaped electromagnets placed in parallel, the ring core
would have N and S poles opposite each other.
And going back to my description of the domain wall moving along
the core, opposite sides of the wall have opposite polarity, so
the wall is a magnetic pole. The flux must escape radially
from the core at this point. This raises an interesting
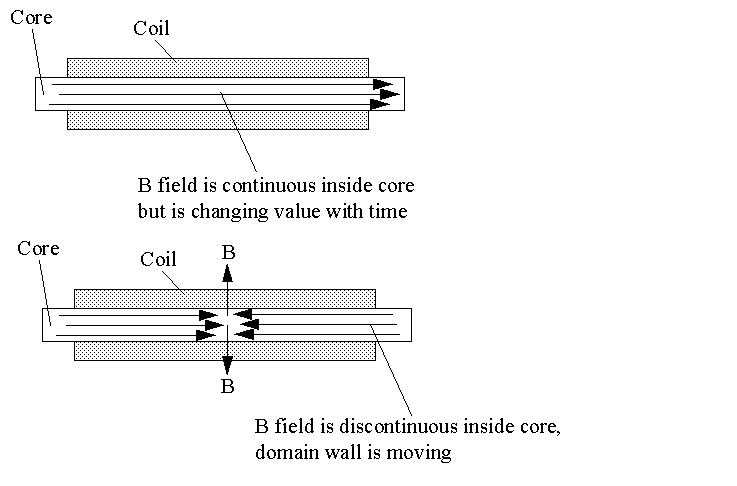
debate concerning transfromer action. In the attached gif
the top picture shows the usual interpretation for transformer
induction. The B lines through the core are continuous,
they change with time to induce voltage in the coil. This
is the induction theory we all love or hate. My second
picture shows what I believe is happening inside an anisotropic
core like metglas, nanoperm and others. I show here just
one domain wall because that is what happens in the MEG.
The B field can not be continuous through the core because the
magnetisation each side of the wall is of opposite polarity.
So the B lines escape. Now to get the voltage induced in
the core we need something different from our usual formulae.
Maybe this is the route to understanding ou.
I gave a formula for the A field due to a domain wall, and this
could be used for the induced voltage if the domain velocity is
known (you would have to integrate over the length of the coil).
The domain velocity can be controlled by the driving waveform (after
all it is possible for the wall to be held stationary with
suitable DC, it doesn't just move by itself). So at low
frequencies, and for coils wound over significant lengths of the
core (which you would normally do for power transformers), the B
induction would be seen to obey normal transformer rules.
But at higher frequencies there will be a velocity limit set by
the material. I have seen on Aspden's site an analysis for
the Hans Coler machine where he equates domain velocity to stress
waves (acoustic velocity) in the material. I bow to
Aspden's superior knowledge, and would point out that the 40kHz
frequency for Bearden's MEG is not unreasonable for this velocity.
Finally I have available some ferrite ring and C cores.
Some of the ring cores are square loop (with the magnetostriction
effect which can shatter the core of driven at mechanical
resonance). Others are not. I will experiment with
the MEG coil configuration, and with the core placed between my
two big slab magnets. When I get time, which will probably
be into December.
Best regards
Cyril Smith
![]() cyrilsmith@camelot64.fsnet.co.uk
cyrilsmith@camelot64.fsnet.co.uk
| Sujet : | MEG |
| Date : | 12/11/00 11:28:07 Paris, Madrid |
| From: cyrilsmith@camelot64.fsnet.co.uk (Cyril Smitht | |
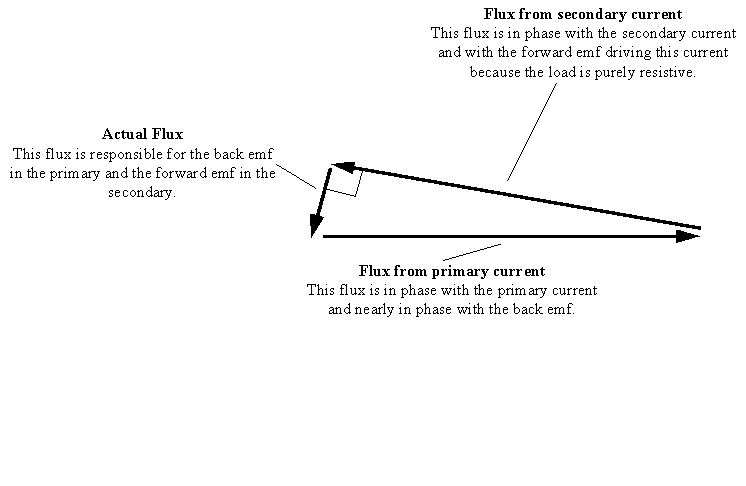
The gif above shows the phasor diagram for a transformer. The fluxes from the primary and secondary currents almost cancel, but not quite. What remains is the actual flux in the core which drives the emf's. The secondary current (and flux vector) is in phase with the induced emf (because the load is resistive). The primary current (and flux vector) is almost in phase with the induced emf, so the primary impedance as seen by the input source is almost resistive: the small phase angle here is the inductive component needed to "create" the actual flux. As you reduce the load resistance you get greater primary and secondary current, so these two flux vectors get bigger (assuming the source can drive the increased power). But you can't do this ad infinitum. The power transfer limit is reached, not by the core's ability to carry the flux (for a given voltage the flux swing is constant, independant of the power transferred), but by the copper losses.
The above is for classical transformer design. With the MEG, I am not so sure that classical procedures apply, as you will see from my other mails.
Regards
Cyril Smith
![]() cyrilsmith@camelot64.fsnet.co.uk
cyrilsmith@camelot64.fsnet.co.uk
Read the previous paper from Cyril Smith
Return to the MEG project home page