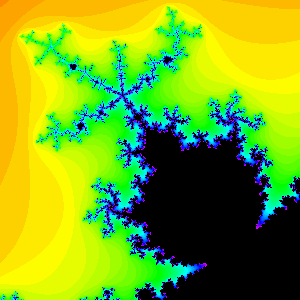
The 2/5 bulb Click here to see an animation of a cycle in the 2/5 bulb.

Figure 5. The 3/7 bulb. Click here to see an animation of a cycle in the 3/7 bulb.
There is a second method to determine p/q, which is not quite well defined but which, in practice, is easier to use. Again compute Jc and the attracting cycle. As before, this cycle determines q regions in the interior of Jc which are joined at wc. Now 0 lies in one of these regions. Note that this region is the largest of the q regions. Now find the "smallest" of the remaining regions. This region is located exactly p/q revolutions about wc in the counterclockwise direction, again yielding the rotation number.
The reason why this region is smallest is that it contains Fc(0), the image of the critical point of Fc. Since 0 is the only critical point for Fc, the region containing 0 suffers the most amount of contraction as we apply Fc, making its image the smallest.
The reason for the imprecision here is in the word "smallest." How do we measure the size of these regions? It is in general impossible to determine the areas of these regions explicitly. Thus in practice we merely "eyeball" the various regions to see which is smallest. Also, when determining p in this fashion, it is best to choose c near the center of the bulb (as near as possible to the c-value for which 0 lies on the attracting cycle). Of course, when q is large, it is essentially impossible to distinguish the smallest region, so we must resort to the previous method in these cases.
There is a third way to determine p that does not involve computing Jc but rather involves only looking at the antenna attached to the bulb in M. The disadvantage of this method is that we sometimes need "hyperbolic eyeglasses" to view the antenna to read off p. That is, this method does not work for all bulbs. To find p, note that there are q spokes emanating from the junction point in the main antenna attached to the bulb. Locate the shortest of these. For most bulbs, this shortest spoke is located p/q revolutions in the counterclockwise direction from the main spoke.
Now this is not always true if we measure the length using the usual Euclidean distance. Rather, we should use a distance that assigns a shorter length to the spokes closer to the main spoke. Without being precise, this is what we mean by "hyberbolic eyeglasses." In Figure 6 we have displayed the p/q bulbs for various choices of p and q. Click on the appropriate figure to view.
To test your ability to read off the rotation numbers, click here for a "clickable" version of Figure 6a-d which is in turn linked to enlargements and movies.
 5 How to Count (Next Section)
5 How to Count (Next Section) Fractal Geometry of the Mandelbrot Set (Cover Page)
Fractal Geometry of the Mandelbrot Set (Cover Page) 3 Periods of the Bulbs (Previous Section)
3 Periods of the Bulbs (Previous Section)