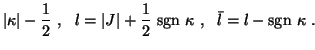Next: The fermionic bag constant
Up: Calculation
Previous: Calculation
Under the condition, that
the free-space vacuum energy vanishes, we obtain the angular
integrated form of the canonical
vacuum energy density
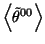 as
as
Thereby, jl denotes the spherical Bessel function,
and the subscripts n, 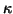 ,
and
,
and 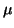 stand for
the radial quantum number, the Dirac
quantum number, and the angular momentum projection, respectively.
The radial quantum number
stand for
the radial quantum number, the Dirac
quantum number, and the angular momentum projection, respectively.
The radial quantum number 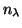 labels the mode energy closest to
labels the mode energy closest to
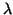 ,
and
,
and
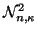 is a normalization constant (see Ref. [21]).
In Eq. (1) the integral over k corresponds to
the free-space subtraction.
Hard fluctuations are excluded by
distinguishing two cases: 1) hard fluctuations with
is a normalization constant (see Ref. [21]).
In Eq. (1) the integral over k corresponds to
the free-space subtraction.
Hard fluctuations are excluded by
distinguishing two cases: 1) hard fluctuations with
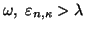 or
or
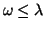 ,
,
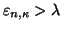 are omitted by
truncation of the mode sum, and 2) hard fluctuations with
are omitted by
truncation of the mode sum, and 2) hard fluctuations with
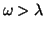 ,
,
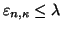 are discarded
by restriction of the z-integration.
The canonical vacuum energy E is given by
are discarded
by restriction of the z-integration.
The canonical vacuum energy E is given by
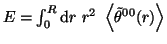 .
.



Next: The fermionic bag constant
Up: Calculation
Previous: Calculation
Marc Schumann
2000-10-16
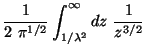
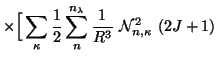
![$\displaystyle -\sum_{l}\ \frac{4}{\pi}\ (2l+1)
\int_0^{\lambda}dk\ k^2 (j_l(kr))^2\ \mbox{e}^{-zk^2}\,\Big]\ ,$](img16.gif)