2 Role of the Critical Orbit

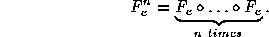
The orbit of 0 plays an important role in determining the structure of Jc. The following fact was discovered by P. Fatou and G. Julia.

Fundamental Dichotomy. If the critical orbit tends to infinity under iteration of Fc, then Jc is a Cantor set. If the critical orbit does not escape, then Jc is a connected set.

The previous paper in this series [1] contains additional details about this fact. It is well known that a Cantor set consists of uncountably many points, and each connected component of a Cantor set is a point. Thus the filled Julia sets of Fc fall into one of two classes, those that consist of a single piece, and those that consist of uncountably many disjoint pieces. It is the orbit of 0 that distinguishes which class c lies in, so the Mandelbrot set may also be defined as the set of c-values for which Jc is connected.

There is a second reason why the orbit of 0 plays a critical role. Suppose Fc admits an attracting cycle of period n. Recall that this means that there is a seed x0 for which

Fcn (x0) = x0 and |(Fcn)' (x0)|

Here Fc^n denotes the n-fold composition of Fc with itself, i.e.,

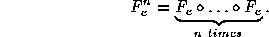
If there exists such an attracting cycle for Fc, then the fact is that the orbit of 0 must tend to this cycle. As a consequence, Fc can have at most one attracting cycle. A quadratic polynomial always has infinitely many cycles, but at most one of them can be attracting.

next 3 Periods of the Bulbs (Next Section)
up Fractal Geometry of the Mandelbrot Set (Cover Page)
previous 1 Basic Definitions (Previous Section)