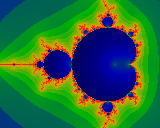
 This image shows the Mandelbrot set, and stops iteration at N=210.
Note the fairly wide strip of 'undecided' area separating the interior
from the boundary.
(Click on the image to view a larger version of the same.)
This image shows the Mandelbrot set, and stops iteration at N=210.
Note the fairly wide strip of 'undecided' area separating the interior
from the boundary.
(Click on the image to view a larger version of the same.)
 If we write the iterated Mandelbrot equation as so:
Zn+1 = Zn2 + c, then, realizing that it
is parameterized by c, we can take its derivative:
Z'n+1 = dZn+1/dc = 2 Z'n Zn + 1.
The second derivative follows:
Z''n+1 = d2Zn+1/dc2 =
2 (Z''n Zn + Z'n2).
Note that Zn, Z'n and Z''n are well
defined for all values of c and finite n: they are entire functions,
'merely' polynomials in c.
For several reasons, it is easier to work with the normalized versions
of these derivatives: define
Pn = Z'n / Zn
and define
Qn = Z''n / Zn.
Note that Pn and Qn are also well defined, being
ratios of polynomials, and containing at most a finite number of poles
and zeros. Again, they are defined both inside and outside and on the
boundary of the Mandelbrot set.
This image shows the Modulus Mn of Qn:
Mn = sqrt ((Re Qn)2 +
(Im Qn)2). It is the dramatic difference
between the interior and exterior of this image that form the
basis of further exploration on this web page.
(Actually, the image shows the logarithm of M4153, where
red is mapped to about log(M)=21, passing through yellow, green,
and down to blue-black at log(M)=-4.
Taking the logarithm helps compress the color space, and bring out
subtle details, especially in the interior. )
If we write the iterated Mandelbrot equation as so:
Zn+1 = Zn2 + c, then, realizing that it
is parameterized by c, we can take its derivative:
Z'n+1 = dZn+1/dc = 2 Z'n Zn + 1.
The second derivative follows:
Z''n+1 = d2Zn+1/dc2 =
2 (Z''n Zn + Z'n2).
Note that Zn, Z'n and Z''n are well
defined for all values of c and finite n: they are entire functions,
'merely' polynomials in c.
For several reasons, it is easier to work with the normalized versions
of these derivatives: define
Pn = Z'n / Zn
and define
Qn = Z''n / Zn.
Note that Pn and Qn are also well defined, being
ratios of polynomials, and containing at most a finite number of poles
and zeros. Again, they are defined both inside and outside and on the
boundary of the Mandelbrot set.
This image shows the Modulus Mn of Qn:
Mn = sqrt ((Re Qn)2 +
(Im Qn)2). It is the dramatic difference
between the interior and exterior of this image that form the
basis of further exploration on this web page.
(Actually, the image shows the logarithm of M4153, where
red is mapped to about log(M)=21, passing through yellow, green,
and down to blue-black at log(M)=-4.
Taking the logarithm helps compress the color space, and bring out
subtle details, especially in the interior. )
 This image shows the Mandelbrot set, and stops iteration at N=210.
Note the fairly wide strip of 'undecided' area separating the interior
from the boundary.
(Click on the image to view a larger version of the same.)
This image shows the Mandelbrot set, and stops iteration at N=210.
Note the fairly wide strip of 'undecided' area separating the interior
from the boundary.
(Click on the image to view a larger version of the same.)
 Same image as above, but iterated to N=4210. Note how the 'undecided'
area has narrowed dramatically.
Same image as above, but iterated to N=4210. Note how the 'undecided'
area has narrowed dramatically.
 The horns tend to be a particularly troublesome area. This image helps
demonstrate that the algorithm behaves well near the horns. Note
that the more optimistic test Mn < n/log(n) fails near
the horns (that image is not shown, but you are welcome to discover that
on your own). This image also illustrates that it is quite
conservative, and tends to keep a good distance from the boundary of the
set. As such, it is both a relief and rather irritating: on the one
hand, it seems clearly safe, and on the other, it would be far more
adventurous if it were a bit more flirtatious.
The horns tend to be a particularly troublesome area. This image helps
demonstrate that the algorithm behaves well near the horns. Note
that the more optimistic test Mn < n/log(n) fails near
the horns (that image is not shown, but you are welcome to discover that
on your own). This image also illustrates that it is quite
conservative, and tends to keep a good distance from the boundary of the
set. As such, it is both a relief and rather irritating: on the one
hand, it seems clearly safe, and on the other, it would be far more
adventurous if it were a bit more flirtatious.
Its possible that a higher derivative might converge faster; however,
what we really want is something that clearly starts filling in the
smaller buds visible in this picture. The fact that this computation is
'safe' near the horns seems to also prevent it from filling up small
buds.
 Coverage of the 'baby' at (re,im)=(-1.765, 0) after 2150 iterations.
Coverage of the 'baby' at (re,im)=(-1.765, 0) after 2150 iterations.
 Coverage of the 'baby' at (re,im)=(-0.16, 1.033) after 2150 iterations.
Coverage of the 'baby' at (re,im)=(-0.16, 1.033) after 2150 iterations.
 Coverage of the 'baby' at (re,im)=(-0.16, 1.033) after 12340 iterations.
Its slow going, but the area does slowly fill up.
Coverage of the 'baby' at (re,im)=(-0.16, 1.033) after 12340 iterations.
Its slow going, but the area does slowly fill up.
Although more experimentation is clearly called for, this preliminary work seems to establish that this algorithm at least never mis-identifies exterior points.
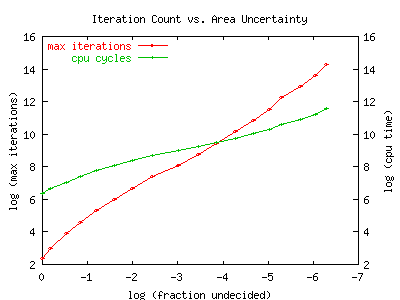 The graph seems to indicate that it does: not terribly fast, but maybe
good enough.
The graph is a log-log plot of the maximum iteration count vs.
fraction of undecided pixels (undecided/(interior+undecided)).
The fraction of undecided pixels can be thought of as an uncertainty
of the area of the Mandelbrot set: its the fraction of the area
which hasn't been determined to be inside or outside the set.
As more and more iterations are performed,
the fraction of ambiguous pixels drops.
The graph appears to be nearly linear, with a slope of about 1.7.
We conclude that this algorithm obtains
successive digits in area of the Mandelbrot
in non-polynomial time: specifically, to get M decimal digits of
precision in the area, we need to iterate exp (1.7*log(10)*M) times.
The graph seems to indicate that it does: not terribly fast, but maybe
good enough.
The graph is a log-log plot of the maximum iteration count vs.
fraction of undecided pixels (undecided/(interior+undecided)).
The fraction of undecided pixels can be thought of as an uncertainty
of the area of the Mandelbrot set: its the fraction of the area
which hasn't been determined to be inside or outside the set.
As more and more iterations are performed,
the fraction of ambiguous pixels drops.
The graph appears to be nearly linear, with a slope of about 1.7.
We conclude that this algorithm obtains
successive digits in area of the Mandelbrot
in non-polynomial time: specifically, to get M decimal digits of
precision in the area, we need to iterate exp (1.7*log(10)*M) times.
The second line of the graph shows the actual number of CPU cycles
needed to compute to a certain level of uncertainty. The slope appears
to be about 0.8: that is, to get M decimal digits of precision in the
area, we need to iterate for exp (0.8*log(10)*M) CPU cycles.
The lesser slope indicates that
the algorithm allows us to stop iterations early
inside the set, and we need to iterate to the bitter end only near the
boundary. However, the time spent iterating near the boundary
quickly dominates the total CPU time: time spent deep in the interior
becomes relatively small. We can conjecture that CPU time spent
in some region is somehow related to some local/average fractal
dimension or complexity, or vice verse might be used to define
a local complexity measure.
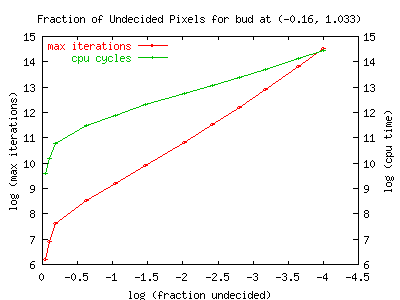 This graph shows iteration count and cpu time vs. the fraction of
undecided pixels for a baby. The baby is the same as that shown
pictorially, above. This is (one of ?? the??) largest baby that
doesn't lie on the Re=0 axis. Note it takes considerably more
cycles/iterations to start filling this in. However, the slope
seems to be about the same: 1.75, which matches within measurement
errors.
This graph shows iteration count and cpu time vs. the fraction of
undecided pixels for a baby. The baby is the same as that shown
pictorially, above. This is (one of ?? the??) largest baby that
doesn't lie on the Re=0 axis. Note it takes considerably more
cycles/iterations to start filling this in. However, the slope
seems to be about the same: 1.75, which matches within measurement
errors.
The slope of the cpu-usage line is about 0.9 which is similar to but
slightly larger than what it was for the overall blob. I wonder if
ever-smaller features become increasingly computationally challenging?
Is the increase of the slope due to the challenge of the exterior, or
the interior, or both?
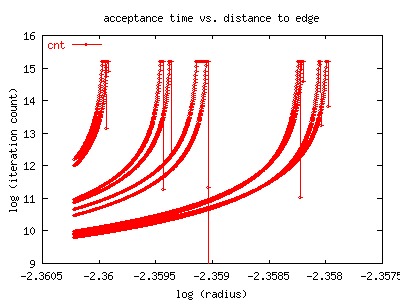 The upper graph shows how many iterations it took before a point was
determined to be in the 'interior', by the measure described above.
It can be clearly seen that as the edge is approached, the number
of iterations needed to determined the membership of the point increases
disastrously. Note that this is a log-log graph, and rather than being
straight, it seems to have poles.
The upper graph shows how many iterations it took before a point was
determined to be in the 'interior', by the measure described above.
It can be clearly seen that as the edge is approached, the number
of iterations needed to determined the membership of the point increases
disastrously. Note that this is a log-log graph, and rather than being
straight, it seems to have poles.
An alternative but undependable
method of determining if a point lies inside the M-set is to
attempt to detect if its orbit settled down to a cycle.
This method is undependable in that there is seemingly no way to decide
whether the orbit is indeed a cycle: there are exterior points which
come arbitrarily close to being cycles for arbitrarily long periods of
time, before diverging away. Although looking for cycles is
an undependable way to identify interior points, it is interesting
to compare convergence rates of this and the second-derivative method.
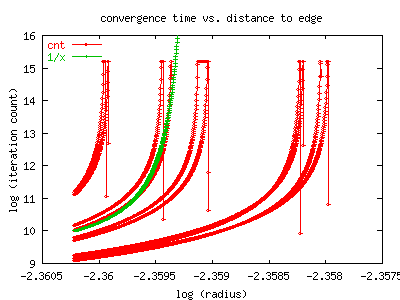 For this bud, we measure convergence to the limit 3-cycle by counting iterations
until the cycle got to within 1e-10 of itself.
This figure shows that convergence to the limit cycle also becomes extremely
slow as one approaches the boundary of the M-set.
As the edge of the bud is approached, the
number of iterations explodes far worse than exponentially, and then some.
Note this is a log-log graph. Just for comparison, the green line, labelled
'1/x', shows what a pole in the log would look like in comparison; that is,
its a graph of exp(1/(0.0945-radius)). (The approximate radius of this bud is
0.0945, see The Bud Page for details).
Although we haven't really taken the time to fit properly or correctly,
the divergence looks about that bad or possibly worse.
For this bud, we measure convergence to the limit 3-cycle by counting iterations
until the cycle got to within 1e-10 of itself.
This figure shows that convergence to the limit cycle also becomes extremely
slow as one approaches the boundary of the M-set.
As the edge of the bud is approached, the
number of iterations explodes far worse than exponentially, and then some.
Note this is a log-log graph. Just for comparison, the green line, labelled
'1/x', shows what a pole in the log would look like in comparison; that is,
its a graph of exp(1/(0.0945-radius)). (The approximate radius of this bud is
0.0945, see The Bud Page for details).
Although we haven't really taken the time to fit properly or correctly,
the divergence looks about that bad or possibly worse.
On the basis of these graphs, it looks like the convergence of this measure is no better, and no worse, than idea of trying to detect a limit cycle. The advantage here is that the new algorithm is both a lot simpler, and seems to actually be reliable. The simplicity is clear: one does not need to guess at the period of the limit cycle one is looking for. The reliability is paramount though: exterior points that are close to the boundary will also appear to approach a limit cycle, and stay there for an arbitrarily long time, before diverging away. Without something like the second derivative, there is no way to decide if a limit cycle has been converged upon.
This algorithm might be used to estimate the area of the Mandelbrot Set. Note that it counts the area of the babies, as well the main blob. I believe that the problem of solving for the area of the Mandelbrot set is still an 'open problem' in mathematics. It's not clear (to me) if/how this algorithm does anything to move forward on that problem.
Note that this algorithm is something like three orders of magnitude 'slower' than simply taking the area of the Mandelbrot set as everything that isn't escaped. That is, if a plain-old iteration produces 6 pixels of uncertainty, then this algorithm will still have something like 6000 pixels of uncertainty. That this is so should be quite dramatically clear from the pictures above, if you look at them & think: the M-set outline is rather crisp & sharp in all of these pictures, whereas there are still huge yellow areas of uncertainty.
Another possibility is to compute the 'plateau'. This seems possible but difficult for the main blob. However, I am not aware of any algorithms that will also compute the baby-blobs.
Copyright © 2000 Linas Vepstas

Undecidably Inside
by Linas Vepstas is licensed under a
Creative Commons
Attribution-ShareAlike 4.0 International License.