|
|
Medias Aritmónica, Aritmética,
Armónica,
Geométrica y Dorada
En general, todas las medias como casos particulares de un concepto
mucho más general: "La Media Racional".
Algunos ejemplos extraídos del libro: “LA QUINTA OPERACIÓN ARITMÉTICA, Revolución del Número” ISBN:
980-07-6632-4. Copyright ©. Todos los derechos reservados. Autor: D. Gómez.
CONTENIDO DE ESTA PAGINA:
- Media Aritmética (Ar)
- Media armónica (Hm)
- MEDIA ARITMONICA (ATM)
- Media Geométrica
- Media Dorada (Fibonacci)
- Conclusiones
- e-MAIL:
Media Aritmetica (Ar)
La media aritmética se obtiene mediante la Media Racional entre fracciones que tienen denominadores iguales. Como ejemplo, la media aritmética entre tres valores 4/3, 5/4, 6/5 es la Media Racional (Mr) entre ellos haciendo previamente que sus denominadores sean iguales:
![]()
![]()
Harmonic
Mean (Hm)
La Media Armónica se obtiene mediante la Media Racional entre fracciones que tienen denominadores iguales. Como ejemplo, la media aritmética entre tres valores 4/3, 5/4, 6/5 es la Media Racional (Mr) entre ellos haciendo previamente que sus numeradores sean iguales:
![]()
![]()
Media Aritmonica (ATM)
La Media Aritmónica ATMi de orden i entre n valores arbitrarios es la Media Racional entre ellos haciendo previamente que los numeradores desde la primera fracción hasta la i-ésima fracción sean iguales, mientras que los denominadores desde la i-ésima fracción hasta la última sean iguales. Entre n valores positivos cualesquiera existen entonces n medias aritmónicas.
A modo de ejemplo, dados cuatro valores 9/8, 2, 2, 2 las sucesivas cuatros medias aritmónicas del primero, segundo, tercero y cuarto orden (ATM1, ATM2 , ATM3, ATM4 ) son las siguientes:
![]()
![]()
![]()
![]()
Como una propiedad bastante interesante note que
9/8* 2* 2* 2= 9, igual que el producto:
![]()
Esto significa que de la misma manera que los
cuatro valores iniciales 9/8, 2, 2, 2 definen --por defecto y por exceso--
la raíz cuarta de 9, también las cuatro medias aritmónicas son
aproximaciones más cercanas --por defecto y por exceso-- a la misma raíz
cuarta de 9.
![]()
Media Geometrica (Gm)
Ver Resolución de raíces.
![]()
Media Dorada (Golden Mean)
El número irracional:
![]()
conocido como la Media Dorada (número que
satisface la Proporción Dorada: p/q= q/(p+q)) es una solución de la ecuación x2+x-1=0
y está relacionada con la famosa secuencia de Fibonacci: 1, 1, 2, 3, 5, 8,
13,...
Dados los siguientes dos radios iniciales:
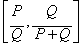
El Proceso Racional para aproximar el vaor
irracional de la Media Dorada es:
(Nota: El acrónimo "Mr" significa
Media Racional)
Paso 1:
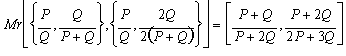
Paso 2:
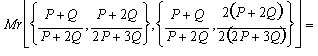
![]()
Paso 3:
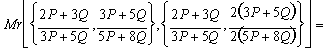
![]()
Paso 4:
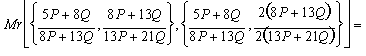
![]()
y así sucesivamente...
en cada etapa del proceso nosotros obtenemos dos aproximaciones cada vez más cercanas al valor de la Media Dorada. Note que los coeficientes numéricos muestran la famosa secuencia de Fibonnaci.
![]()
Conclusiones
Con base al nuevo concepto general de la Media Racional, está claro que el credo tradicional sobre "Medias" debe ser redefinido. Es realmente inquietante y preocupante el comprender que este concepto general de la media racional evidenciado en los ejemplos anteriores, haya pasado desapercibido a lo largo de toda la historia de las matemáticas, y muy especialmente si consideramos que, por ejemplo, la Media Aritmónica es una herramienta aritmética indispensable para la aproximación de raíces mediante métodos con velocidad de convergencia de ordenes superiores al segundo.
![]()
Copyright
©
Todos los derechos reservados bajo las convenciones internacionales de derechos de autor. Ninguna parte de estas páginas pueden ser reproducidas, almacenadas o transmitidas en cualquier forma o por cualquier medio sin la previa autorización del autor: D. Gómez.
Last
revision: 2002.