Resolución de raíces y la Media Racional

Algunas muy breves observaciones y ejemplos extraídas del libro:   “LA QUINTA OPERACIÓN ARITMÉTICA, Revolución del Número” ISBN: 980-07-6632-4.  Copyright ©. Todos los derechos reservados. Autor: D. Gómez.

 

CONTENIDO:

Nota: En esta página el acrónimo Mr debe ser interpretado como Media Racional (Rm).

Todos los ejemplos expuestos aquí responden a un mismo principio general  el “Proceso Racional” basado en la simple operación aritmética “Media Racional” y han sido escogidos para mostrar brevemente el alcance de este nuevo y elemental concepto aritmético que estuvo al alcance de cualquiera desde tiempos ancestrales, sin embargo para nuestra sorpresa no existen precedentes sobre estos simples y eficientes métodos aritméticos. El lector estará entonces en libertad de crear una inmensa variedad de nuevas funciones de iteración para la resolución de ecuaciones algebraicas, sin uso del sistema Cartesiano, ni decimales, ni derivadas.

 

 

 

• La resolución de raices y el Proceso Racional
• Preliminares
• El Proceso Racional (RP-1) de aproximación a la raíz cúbica de 2
• Otro Proceso Racional (RP-2), relacionado con el método de Bernoulli
• Proceso Racional Acelerado ARP-2a
• Proceso Racional Process ARP-2b

• Formulación trivial de los métodos de Newton y Halley por medio del Proceso Racional
• Raíz cuadrada de P, Método de Newton como simple proceso racional
• Raíz cuadrada de P, Método de Halley como simple proceso racional
• Raíz cúbica de P, Método de Newton como simple proceso racional
• Raíz cúbica de P, Método de Halley como simple proceso racional
• Raíz cuarta de P, Método de Newton como simple proceso racional
• Raíz cuarta de P, Método de Halley como simple proceso racional
• Raíz quinta de P, Método de Newton como simple proceso racional
• Raíz quinta de P, Método de Halley como simple proceso racional
• Expresión general del Método de Halley a partir del proceso racional
• Infinito número de nuevas funciones de iteración mediante el proceso racional
• Conclusiones

Resolución de raíces y el Proceso Racional

La verdadera historia acerca de la resolución de raíces

Aún a pesar de los primeros intentos de aproximación numérica de raíces realizados por:

 

• Babilonios (1600 B.C.) quienes trabajaron con la raíz cuadrada de 2 (1+ 24/60 +51/60² + 10/60³, Yale No. 7289).

 

•Los matemáticos chinos (250 B.C.) quienes desarrollaron un método no-natural de ensayo y error para resolver raíces basado en geometría (gnomons), los cuales eran demasiado difíciles de utilizar (por no decir imposible) para raíces de grado superior al segundo hasta el descubrimiento muy posterior que ellos mismos hicieron del diagrama de coeficientes binomiales mal conocido  en estos días como el "Triángulo de Pascal".

 

•Los griegos quienes aparentemente trataron de resolver raíces cúbicas también mediante el uso exclusivo de geometría  (Heron, Menaechmus) sin dejar rastros para nosotros de ningún algoritmo de iteración ni alguna aproximación numérica aún para la raíz cuadrada de 2.

no existen evidencias de algún método natural (contrario al ensayo-&-error) para resolver raíces superiores al segundo grado desde los  Babilonios hasta la creación de los decimales y el sistema cartesiano, aún simples aproximaciones numéricas a la raíz cúbica son muy difíciles de encontrar.

La siguiente lista muestra algunas de las personas que a lo largo de la historia trataron de encontrar procesos de ensayo-&-error o simplemente aproximaciones. (Nota: Es necesario conocer muy bien la diferencia filosófica que existe entre
un método natural y un método de ensayo-&-error):

•Babylonians (1600 B.C.)

•Sulbasutras (500 B.C.)

•Chi-Chang Suan-Shu, Nine Chapters (250 B.C.)

•Archimedes (225 B.C.)

•Heron (1st. century)

•Chan Heng (130)

•Chao Chung Ching (200)

• Berlin Papyrus (2nd.century)

•Theon of Alexandria (390)

•Wang Hsiao Tung (625)

•Brahmagupta (628)

•China, Ten manuals (656)

•al-Kharkhi(1020)

•Fibonacci(1202)

•Chiu Chiu Sao, Nine Sections (1247)

•Li Yeh (1248)

•Yang Hui (1261)

•Planudes (1300)

•Chu Shih Chieh (1303)

•Rhabdas (1340)

•Narayana (1350)

•Rama (1450)

•Chuquet(1484)

•Pacioli and Roche (1500-1520)

•Tonstall (1522)

•Fine (1525)

•Stifel (1544)

•Buteo (1559)

•Clavius (1585)

•Girard (1634)

En todos esos intentos a lo largo de toda la historia podemos encontrar siempre una muy extraña insistencia en tratar de resolver los problemas propios del Número mediante el uso de un sistema extrínseco a éste como lo es la Geometría dando además como resultado algoritmos no naturales de ensayo-&-error. Para su sorpresa, el lector comprobará que todos esos problemas sobre resolución de raíces que siempre fueron interpretados y aproximados de alguna manera mediante el uso del sistema cartesiano, los decimales y los infinitesimales, podían haber sido formulados y desarrollados exclusivamente mediante el uso de simple Aritmética (Media Racional).

 

Preliminaries

Es realmente sorprendente comprender que el Número por sí mismo nos brinda  el más simple camino para aproximar raíces. En este sentido, la muy antigua secuencia:

analizada por Nicomachus en su “Introduction to Arithmetic” y definida como “números superparticulares” brinda a la luz la siguiente propiedad:

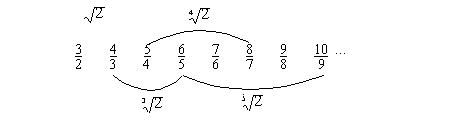
En la figura 4.1 podemos ver un conjunto de dos fracciones [3/2, 4/3] cuyo producto es trivial e igual a 2, esto es, dos aproximaciones por defecto y exceso a la raíz cuadrada de 2.

También otro conjunto [4/3, 5/4, 6/5] cuyo producto es trivial e igual a 2, esto es, tres aproximaciones por defecto y por exceso a la raíz cúbica de 2.

Otro conjunto [5/4, 6/5, 7/6, 8/7] cuyo producto es trivial e igual a 2, esto es, cuatro aproximaciones por defecto y por exceso a la raíz cuarta de 2.

Otro conjunto [6/5, 7/6, 8/7, 9/8, 10/9] cuyo producto es trivial e igual a 2, esto es, cinco aproximaciones por defecto y por exceso a la raíz quinta de 2.

y así sucesivamente...

Sin embargo, esta muy simple conexión entre esa secuencia y la resolución de raíces pasó inadvertida para Nicomachus.

¿Es que acaso los números necesitan decirnos algo más?
Re: Por supuesto que no!
Nosotros necesitamos solamente un conjunto de n fracciones iniciales cuyo producto sea P para encontrar un proceso racional y natural basado en la Media Racional para aproximar la n-ésima raíz de P. Podríamos usar un número infinito de conjuntos similares a los indicados por la serie de los superparticulares, pero por supuesto por ahora seleccionaremos solamente dos tipos de conjuntos que cumplen las características mencionadas:

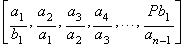
En las siguientes secciones veremos:
Algunos ejemplos numéricos sobre algunos muy simples procesos racionales para calcular específicamente la raíz cúbica de 2, de manera que el lector podrá apreciar que los antiguos matemáticos tenían al alcance de la mano las herramientas aritméticas más elementales para la resolución de problemas relacionados de alguna manera con lo que llamamos hoy en día "resolución de ecuaciones algebraicas de cualquier grado".

 

Proceso racional (RP-1) de aproximación a la raíz cúbica de 2

(Nota: El acrónimo Mr debe ser interpretado como: Media Racional (Rm)

Dado el conjunto inicial de tres valores:

cuyo producto es trivial e igual a 2. De acuerdo a nuestra notación para la  media racional, el proceso racional de aproximación  a la raíz cúbica de 2 es así:

y así sucesivamente...

En cada paso, obtenemos un nuevo conjunto de tres aproximaciones (cuyo producto es trivial e igual a  2) por defecto y exceso a la raíz cúbica. Es necesario resaltar que para desarrollar este proceso racional natural no hicimos uso de decimales, ni ensayo-&-error, ni sistema cartesiano, ni los infinitesimales.

Podemos expresar ese proceso racional de una manera más general:

Dado el conjunto inicial de tres valores:

el proceso racional hacia la raíz cúbica de P es:

 

Otro proceso racional (RP-2), relacionado con el muy conocido método de Daniel Bernoulli

Dado el conjunto inicial:

El nuevo proceso racional a la raíz cúbica de P:

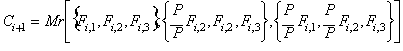
el cual converge levemente más rápido que el anterior, ambos estando directamente relacionados con el conocido método de Bernoulli y las fracciones continuas generalizadas.

Proceso racional acelerado ARP-2a

Dado el conjunto inicial:

Calculando las siguientes medias racionales equivalentes a la media armónica y aritmética respectivamente:

180/143 corresponde a la media armónica, y 227/180 a la media aritmética. Es fácil encontrar un tercer valor v₃, tal que: (180/143)*(227/180)*(v₃) = 2, así, v₃ = (2*143)/227 = 286/227. El nuevo conjunto de tres aproximaciones es:

El valor 286/227 es también una  media racional entre las tres fracciones iniciales, de manera que el proceso se transforma en un algoritmo totalmente automático. Repitiendo sucesivamente los pasos anteriores y escogiendo solamente la tercera aproximación de cada nuevo conjunto obtenemos la siguiente tabla que incluye una comparación con los valores que se obtendrían al usar el conocido método de Newton:

Proceso Racional Acelerado  (ARP-2a)		Método de Newton
Aproximaciones: xi	Error	Aproximaciones: xi	Error
286  227	9E-6	63  50	8E-5
27825466  22085087	2E-12	375047  297675	-5E-9
25649277607024348370746  20357845127807416346597	7E-26	158262616209301396  125613121728942225	-2E-16

Proceso Racional ARP-2b

Dado el conjunto inicial:

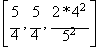
Calculando las siguientes media racionales equivalentes a las media armónica y aritmética:

Es fácil comprobar que un tercer valor v₃, tal que: (160/127)*(63/50)*(v₃)=2, será v₃ = (2*127*50)/(160*63) = 635/504.

(El valor 635/504 es también una media racional entre las tres fracciones iniciales.)

Al evaluar tres pasos y tomar solamente la tercera aproximación de cada nuevo conjunto, obtenemos los siguientes errores: 4 E-7, 3 E-20, 1 E-59,  59 dígitos exactos al valor de la raíz en la tercera iteración.

 

Desarrollo trivial de los métodos de Newton y Halley  mediante el Proceso Racional

Raíz cuadrada de P, el método de Newton como simple proceso racional

Dado el conjunto de dos fracciones:

cuyo producto es trivial e igual a P. Haciendo sus denominadores iguales y calculando luego la media racional (Ar=Media Aritmética):

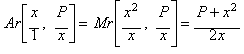
Obtenemos un valor medio entre las dos fracciones iniciales, una aproximación más cercana al valor de la raíz cuadrada de  P, en otras palabras, hemos obtenido una función de iteración equivalente al Método de Newton cuando es aplicado a: x²-P.

Raíz cuadrada de P, método de Halley como simple proceso racional

Dado el conjunto inicial de cuatro fracciones:

cuyo producto es trivial e igual a P², esto es, cuatro aproximaciones a la raíz cuadrada de  P.

Calculando la  Media Aritmónica de tercer orden (ATM₃) entre esos valores iniciales:

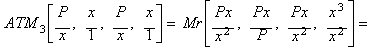
obtenemos un valor medio entre las cuatro fracciones dadas, una aproximación más cercana al valor de la raíz cuadrada de  P, esto es, una función de iteración equivalente al método de Halley cuando es aplicado a la función x² - P.

 

Raíz cúbica de P, método de Newton como simple proceso racional

Calculando la  media aritmética (Ar):

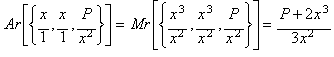
y realizando un análisis similar al de los casos anteriores obtenemos la función de iteración correspondiente al método de Newton aplicado a la función: x³ - P.

 

Raíz cúbica de P, método de Halley como simple proceso racional

Calculando la media aritmónica de segundo grado (ATM₂):

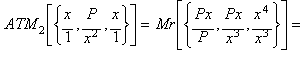
obtenemos la función de iteración equivalente a aplicar el método de Halley a la función: x³- P.

Raíz cuarta de P, método de Newton como simple proceso racional

Dado el conjunto:

de cuatro aproximaciones triviales a la raíz cuarta de  P.

Calculando la  media aritmética (Ar):

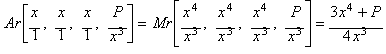
obtenemos la función de iteración correspondiente al método de Newton aplicado a la función x⁴ - P.

 

Raíz cuarta de P, método de Halley como simple proceso racional

Dado el conjunto de valores:

cuyo producto es trivial e igual a P², ocho aproximaciones a la raíz cuarta de P.

Calculando la media aritmónica de quinto orden ATM₅ :

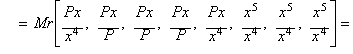
obtenemos la función de iteración equivalente a aplicar el método de Halley a la función: x⁴- P.

 

Raíz quinta de P, método de Newton como simple proceso racional

Dado el conjunto de valores:

La media aritmética es:

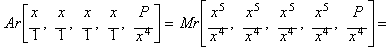
expresión que equivale al método de Newton aplicado a la función:  x⁵ - P.

 

Raíz quinta de P, método de Halley como simple proceso racional

Dado el conjunto:

La media aritmónica de tercer orden ATM₃ da:

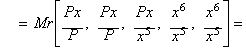
que es la función de iteración del método de Halley aplicado a la función x⁵ - P.

 

Expresión general del método de Halley

Si continuamos con ese proceso de obtención de funciones de iteración para cada una de las raíces entonces podremos obtener la función general de Halley para la raíz de grado n de P:

 

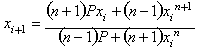
Nuevas funciones de iteración

Utilizando otros tipos de conjuntos iniciales es muy fácil obtener por ejemplo una nueva función de iteración (IF-1) para calcular la raíz n de  P, esa función es:

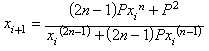
la cual triplica también el número de dígitos exactos en cada iteración.

El lector podrá encontrar también otra función de iteración (IF-2), específicamente diseñada para la raíz cuadrada de P:

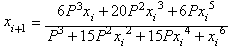
(Podría ser de interés para el lector hallar su expresión generalizada para calcular la raíz n de  P )

Para el caso específico de la raíz cuadrada de 2, esa función nos ofrece los siguientes valores comparados al mismo tiempo con el método anterior y el de Halley:

	FI-1  Process	FI-2  Process	Halley's  Method
i	Errors
1	0.014357	-7.21 E-5	0.014214
2	3.64 E-7	-7.79 E-28	3.64 E-7
3	6.05 E-21	-1.24 E-165	6.05 E-21
4	2.77 E-62	-1.98 E-992	2.77 E-62

 

De esta manera pueden ser generados un infinito número de funciones de iteración.

CONCLUSIONES

Resulta realmente insólito que métodos tan simples como los indicados aquí no aparezcan mencionados en ningún texto sobre números. Basados en estos procesos aritméticos extremadamente simples y considerando la incompresible ausencia de precedentes en esta materia a lo largo de toda la historia matemática, cualquier persona puede comprender ahora que es ciertamente  una ridícula arrogancia el pensar que las artificiales creaciones personales (ej.: sistema cartesiano, fracciones decimales, números imaginarios, etc.) de cualquier individuo egocéntrico pudieran alguna vez sobrepasar el orden natural predeterminado por Dios en acuerdo con las armonías del Número.

[TOP PAGE]

 

Copyright ©

Todos los derechos reservados bajo las convenciones internacionales de derechos de autor. Ninguna parte de estas páginas pueden ser reproducidas, almacenadas o transmitidas en cualquier forma o por cualquier medio sin la previa autorización del autor: D. Gómez.

 

Last revision: 2002.