Media Racional

Algunas definiciones y observaciones de la Media Racional (Mediant generalizada) extraídas del libro: “LA QUINTA OPERACIÓN ARITMÉTICA, Revolución del Número” ISBN: 980-07-6632-4. Copyright ©. Todos los derechos reservados. Autor: D. Gómez.

 

CONTENIDO:

• Media Racional. Definición
• Ejemplo
• Operación Racional General. Definición:
• Comentarios

 

La Media Racional

(Mediant Generalizada)

Media Racional. Definición.

Dado un conjunto V de n números racionales positivos ordenados de acuerdo a sus magnitudes:

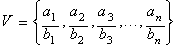
La expresión:

es un valor medio (Media Racional, Rm) entre los valores extremos  (a₁/b₁), (a_n/b_n) del conjunto V:

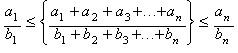
Una notación general para múltiples medias racionales puede ser expresada así:

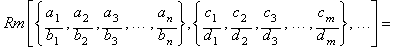
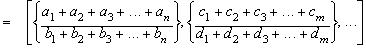
Ejemplo:

El siguiente caso:

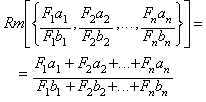
es también la media racional entre los mismos n números racionales, modificando esta vez la forma de cada fracción mediante los factores: F₁, F₂,..., F_n.

Podemos decir que dado cualquier conjunto de n valores escogidos a voluntad (enteros, racionales o irracionales) ordenados en orden creciente:

y dado otro conjunto [F₁, F₂, F₃, . . ., F_n] de valores positivos cualesquiera (enteros, racionales or irracionales), entonces la expressión:

es la Media Racional entre los valores v₁,v_2,v₃, ... ,v_n

Operación General Racional (Gro). Definición:

Podemos ir más lejos aún y definir la Operación General Racional (Gro) (no necesariamente un valor medio dentro del conjunto dado inicialmente) entre n valores arbitrarios v₁,v_2,v₃, ... ,v_n como lo haremos a continuación:
Dados n valores v₁=a₁, v₂=(-a₂/b₂), v₃=(a₃/b₃), v₄=-a_4, . . . , v₅=-a_n , la Gro entre esos valores viene dada así:

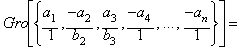
Más aún, dadas n funciones racionales: f₁(x)/g₁(x), f₂(x)/g₂(x), f₃(x)/g₃(x), ..., f_n(x)/g_n(x), la Operación General Racional (no necesariamente un valor medio entre los valores de esas funciones) es:

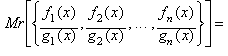
En algunos casos la Gro será la Media Racional entre esas n funciones racionales.

Cualquier algoritmo basado en la Media Racional será llamado en adelante: Proceso Racional.

Es necesario decir que el análisis de la Media Racional (Rm) ha sido restringido –a lo largo de toda la historia de las matemáticas– al caso específico de la operación llamada Mediant (n=2) y algunas curiosas propiedades de las series de  Farey, los círculos de Ford, el árbol de Stern-Brocot  y la generación de los convergentes en las fracciones continuas simples, ejemplo:

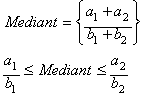
Comentarios

Algunos matemáticos usualmente establecen que está operación no está bien definida dentro del conjunto de los números racionales, esto es, que la media racional trabaja exclusivamente con pares ordenados de enteros en lugar de números racionales. Como ejemplo, calculemos la media racional:

Rm[3/2, 4/3]= 7/5

y calculemos la media racional entre esos mismos números pero cambiando 3/2 por su forma 6/4:

Rm[6/4, 4/3]= 10/7

Se han utilizado los mismos valores, la misma operación y sin embargo el resultado es diferente.

Ahora, si debido a esto nosotros argumentamos que esta operación no está "bien definida" dentro del conjunto de los racionales, entonces deberíamos decir también que las siguientes operaciones matemáticas no están bien definidas dentro del conjunto de los números racionales, principalmente porque la Media Racional es el principio fundamental que las regula:

•La Media Armónica: Es la Media Racional entre fracciones con numeradores iguales.

•La Media Aritmética: Es la Media Racional entre fracciones con denominadores iguales.

•La Media Aritmónica: Es la Media Racional entre fracciones donde un grupo de denominadores y numeradores son iguales de acuerdo a una regla específica.

•Media Geométrica

•Generación de los convergentes de las fracciones continuas generalizadas

•Números transcendentales y algebraicos

•Métodos de Bernoulli, Newton y Halley para la resolución de ecuaciones algebraicas

•Expansiones en series de potencias (series de Maclaurin-Taylor).

•Definición de las operaciones aritméticas de los números irracionales

•Estadísticas

•Centro de gravedad

•Círculos de Ford

•Fracciones de Farey

Contrariamente a la corriente actual de pensamiento de los matemáticos modernos, está claro que todo ese concepto sobre la "buena" o "mala" definición de esta operación dentro del conjunto de los racionales debería ser considerado desde un punto de vista totalmente distinto, puesto que esa visión restrictiva  está basada en una concepción exclusivamente cartesiana de los números y esa no tiene porque ser necesariamente la herramienta ideal para comprender sin distorsiones de ningún tipo la verdadera esencia de la Cantidad y sus diversas manifestaciones.

Así, contrariamente a los fundamentos absolutistas del sistema Cartesiano, el Número no debería ser considerado simplemente como un "Valor Absoluto" (exclusivo valor decimal) sino como una entidad con valor absoluto y valor relativo. De la misma manera que las flores nos brindan múltiples propiedades naturales: belleza, color, aroma, etc. también el Número nos brinda mucho más que un simple "valor absoluto", éste sostiene además un valor relativo (La forma de la fracción) y su localización específica dentro del esquema general de los números. La importancia de todas esas propiedades serán evidentes al lector cuando estudie la nueva operación: Media Aritmónica. Un punto muy importante, corolario de todos las nuevas propiedades y métodos que tienen su base en la simple aritmética de la Media Racional, es el hecho cierto que el sistema Cartesiano ha servido muy especialmente a la despersonalización del Número confinándolo al triste papel de no ser más que un simple valor absoluto (valor decimal).

En verdad es realmente inquietante  comprender que los más antiguos matemáticos (Babilonios, Griegos, etc.) ciertamente tenían al alcance de sus manos la herramienta aritmética más simple y elemental  (La Media Racional) para lograr desarrollar todos esos llamados "algoritmos avanzados" que han sido consagrados como los más resaltantes logros sacados a luz gracias exclusivamente al sistema cartesiano y la creación de los decimales. Basados en todas las evidencias históricas, al parecer la extremadamente simple operación aritmética Media Racional desarrollada brevemente en estas páginas y con más detalle  en el libro “La Quinta Operación Aritmética” no tiene precedentes en toda la larga historia de la resolución de ecuaciones.

De todos los nuevos y elementales procesos aritméticos mostrados en el libro "la quinta operación aritmética" el lector podrá comprender las siguientes importantes consideraciones:

•El sistema cartesiano no puede ser considerado como un sistema fundamental de la filosofía natural sino como una creación artificial que aparte de ser extrínseca a las propiedades naturales de los números, principalmente contribuye a distorsionar y viciar la imagen genuina de la Cantidad relegando al Número al simple papel de un valor absoluto.

•Las operaciones aritméticas de los números irracionales pueden ser definidas de manera muy sencilla mediante el Proceso Racional y basados en el Número en sí mismo en lugar de utilizar las creaciones y opiniones personales de Dedekind y Cantor.

•Las tradicionales fracciones continuas no son más que un caso particular (Fracciones continuas de segundo orden) de una concepción general llamada: “Fracciones contínuas generalizadas” (Fracciones fractales), las cuales producen representaciones periódicas de los números algebraicos de cualquier grado. Cualquier representación de los números irracionales de grado superior al segundo se obtiene totalmente distorsionada cuando se utilizan las tradicionales fracciones continuas “Fracciones continuas de segundo orden”.

•Sorprendentemente no hay muchos precedentes en el análisis de la media racional, casi todos dirigidos exclusivamente al caso especial de la Mediant. Algunas de las personas que trabajaron con esa operación: Nicolas Chuquet (1484), Haros(1802), Farey(1816), Cauchy, J. Wallis, C. S. Peirce, Stern-Brocot(1858-1860), D. Hidalgo (1963). Lester R. Ford y Pick.

•La media racional es la más elemental operación aritmética para la resolución de raíces y también regula las expansiones en series de potencias y la generación de los números transcendentales.

•La Media Aritmónica es un caso particular de la media racional esencial en la resolución de raíces y la cual, basados en todas las evidencias disponibles- parece haber pasado inadvertida a lo largo de toda la historia.

•Basado en todas las observaciones y métodos descritos, resulta entonces una patética arrogancia el pensar que  cualquier producto (números imaginarios, sistema cartesiano, teoría especial de la relatividad, cuarta dimensión, geometrías no-euclideanas, etc.) proveniente de la opiniones y juicios personales de cualquier matemático pueda alguna vez superar el orden natural y las hermosas propiedades determinadas "de acuerdo al número por la mente de Él quién creó  todas las cosas, porque el orden fue establecido, como un esquema preliminar,...” (texto en comillas, traducción personal de: Nicomachus, chap.VI,[1]).

 

[TOP PAGE]

 

Copyright ©

Todos los derechos reservados bajo las convenciones internacionales de derechos de autor. Ninguna parte de estas páginas pueden ser reproducidas, almacenadas o transmitidas en cualquier forma o por cualquier medio sin la previa autorización del autor: D. Gómez.

 

Last revision: 2002.