|
|
Arithmonic, Arithmetic,Harmonic,
Geometric
and Golden Means
All
means as particular cases of a more general concept: "The Rational Mean", some examples extracted from the book:
: “LA QUINTA OPERACIÓN ARITMÉTICA, Revolución del
Número” (Title translation: The Fifth
Arithmetical Operation, Number Revolution) ISBN: 980-07-6632-4. Copyright ©.
All rights reserved under international Copyright Conventions. Author: D.
Gómez.
CONTENTS:
- Arithmetic Mean (Ar)
- Harmonic Mean (Hm)
- ARITHMONIC MEAN (ATM)))
- Geometric Mean
- Golden Mean
- Conclusions
- GO TO &--MAIL
TO:
![]()
Arithmetic
Mean (Ar)
The
arithmetic mean is the rational mean between fractions having equal denominators. As an
example, the arithmetic mean between three values 4/3, 5/4, and 6/5 is the
rational mean between them by previously making their denominators the same:
![]()
![]()
Harmonic
Mean (Hm)
The
harmonic mean is the rational mean between fractions having equal numerators. As an
example, the harmonic mean between three values 4/3, 5/4, and 6/5 is the
rational mean between them by previously making their numerators the same:
![]()
![]()
Arithmonic
Mean (ATM)
The
arithmonic mean ATMi of order i between n
arbitrary values is the rational mean between them by previously making the
numerators of the first fraction up to the i-th fraction the same, and
the denominators of the i-th fraction up to the last one the same. There
are n arithmonic means between n numbers.
As an example given four
values 9/8, 2, 2, 2 the following are the successive four arithmonic means of
the first, second, third and fourth order (ATM1, ATM2
, ATM3, ATM4 ):
![]()
![]()
![]()
![]()
As an interesting property
notice that 9/8* 2* 2* 2= 9 and the product:
![]()
This means that in the same
way as the initial four values 9/8, 2, 2, 2 define --by defect and excess-- the
fourth root of 9, also the four arithmonic means are closer approximations --by
defect and excess-- to the same root.
![]()
Geometric
Mean (Gm)
See roots web page.
![]()
Golden Mean
The
irrational number:
![]()
known as the Golden Mean value
(a number satisfying the golden proportion: p/q= q/(p+q)) is a solution to the
equation x2+x-1=0 and is related to the Fibonacci's sequence: 1, 1,
2, 3, 5, 8, 13,...
Given the following two
initial ratios:
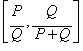
The rational process for approximating the irrational value of the
Golden Mean is:
(Note: The acronym "Mr"
means Rational Mean, Rm)
Step 1:
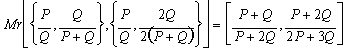
Step 2:
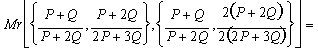
![]()
Step 3:
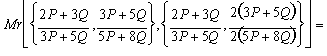
![]()
Step 4:
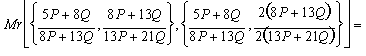
![]()
and so on...
at each stage of the
process we get two closer rational approximations to the Golden Mean. Notice
that the numerical coefficients bring out Fibonnaci's sequence.
![]()
Conclusions
Based on
the new rational mean concept, it is clear that the traditional credo on
"means" should be redefined. It is striking to realize that the above
general concept on the rational mean embracing all the means, have been passed
over all through the history of Arithmetic, specially when considering that,
for example, the Arithmonic Mean is an indispensable arithmetical tool for solving roots by agency of higher order convergence methods.
![]()
Copyright ©
1993-2002
All rights reserved under international
Copyright Conventions.
No part of this page may be reproduced, stored
or transmitted in any form or by any means without the prior permission of the
author: D. Gómez.
Last revision: 2002