|
|
Roots
Solving and The Rational Process
This page contains some
methods and observations extracted from the book: “LA QUINTA
OPERACIÓN ARITMÉTICA, Revolución del Número” (Title translation: The Fifth Arithmetical Operation,
Number Revolution) ISBN: 980-07-6632-4. Copyright ©. All rights reserved under
international Copyright Conventions. Author: D. Gómez.
![]()
CONTENTS:
Note: In
this web page the Spanish acronym: Mr must be interpreted
as Rational Mean (Rm).
All the
examples shown in this page are ruled by the same general principle: “The
Rational Process” based on
the “Rational Mean” and were
chosen in order to show the scope of this new simple arithmetical concepts which
even being within everyone’s reach since ancient times --to our surprise and
astonishment-- have no precedents all through the history of mathematics. So,
the reader will be able to develop a huge amount of new iteration functions for
solving algebraic equations of higher degree by agency of just the most simple
Arithmetic, No Cartesian system, No decimals, No fluxions, at all.
- Trivial
formulation of Newton's and Halley's methods by means of the Rational
Process
- Square root of P, Newton's
method and the rational process
- Square root of P, Halley's
method and the rational process
- Cube root of P, Newton's
method and the rational process
- Cube root of P, Halley's
method and the rational process
- Fourth root, Newton's method
and the rational process
- Fourth root, Halley's method
and the rational process
- Fifth root, Newton's method
and the rational process
- Fifth root, Halley's method and
the rational process
- Halley's method general
expression
- New iteration functions
- Conclusions
![]()
Roots
Solving and The Rational Process
The True Story on Roots
Solving
Even though
the early attempts on roots solving made by:
• Babylonians (1600 B.C.)
who worked with the square root of 2 (1+ 24/60 +51/602 + 10/603,
Yale No. 7289).
•The Chinese (250 B.C.) who
developed a trial and error method for solving roots based on geometry
(gnomons), which was so hard (not to say impossible) to be used for cube and
higher roots until the discovery of the binomial coefficients diagram, nowadays
commonly called “Pascal Triangle”.
•The Greeks who apparently
tried to solve cube roots by means of geometry (Heron, Menaechmus) without
letting us know neither any iteration algorithm nor any numerical
approximation, even to the cube root of 2.
There are no evidences of
any natural method (no trial-&-error) for solving cube roots since
Babylonians up to the creation of decimal fractions and the Cartesian system,
even simple numerical approximations to the cube root are so hard to find.
The following list refers to
people who tried to find trial-&-error methods or even just approximations:
•Babylonians (1600 B.C.)
•Sulbasutras (500 B.C.)
•Chi-Chang Suan-Shu, Nine
Chapters (250 B.C.)
•Archimedes (225 B.C.)
•Heron (1st. century)
•Chan Heng (130)
•Chao Chung Ching (200)
• Berlin Papyrus
(2nd.century)
•Theon of Alexandria (390)
•Wang Hsiao Tung (625)
•Brahmagupta (628)
•China, Ten manuals (656)
•al-Kharkhi(1020)
•Fibonacci(1202)
•Chiu Chiu Sao, Nine
Sections (1247)
•Li Yeh (1248)
•Yang Hui (1261)
•Planudes (1300)
•Chu Shih Chieh (1303)
•Rhabdas (1340)
•Narayana (1350)
•Rama (1450)
•Chuquet(1484)
•Pacioli and Roche
(1500-1520)
•Tonstall (1522)
•Fine (1525)
•Stifel (1544)
•Buteo (1559)
•Clavius (1585)
•Girard (1634)
From all those attempts we
can find a fathomless insistence in trying to solve problems relating Number by
means of Geometry and Trial-&-Error methods. Surprisingly, we are about to
see that even those problems on roots solving which were finally solved by
using the cartesian system, decimals and infinitesimals, can be easily
formulated in terms of the most simple Arithmetic.
![]()
Preliminaries
It is
astonishing to realize that Number by itself bring us the most simple way to
handle roots. In this way, the ancient sequence:
![]()
analyzed and classified by
Nicomachus in his “Introduction to Arithmetic” as “superparticular numbers”
bring the following figure to light:
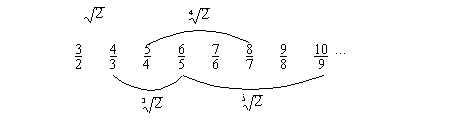
However, even Nicomachus
passed over this very simple connection between superparticular numbers and
roots solving.
In the figure 4.1 we see a
set of two fractions [3/2, 4/3] whose product is trivial and equal to 2, that
is, two approximations by defect and excess to the square root of 2.
Also another set [4/3, 5/4,
6/5] whose product is trivial and equal to 2, that is, three approximations by
defect and excess to the cube root of 2.
Another set [5/4, 6/5, 7/6,
8/7] whose product is trivial and equal to 2, that is, four approximations by
defect and excess to the fourth root of 2.
Also the set [6/5, 7/6,
8/7, 9/8, 10/9] whose product is trivial and equal to 2, that is, five
approximations by defect and excess to the fifth root of 2.
and so on...
Need Number say more?
Of course, Not!. We just
need a set of n initial fractions whose product is P in order to
find a natural rational process (based on the rational mean) for approximating the n-th root
of P. We might use infinitely many sets similar to those brought to light
by superparticular numbers, however, by now let's select the following two
sets:
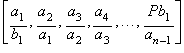
![]()
In the following
sections we'll see:
Some numerical examples on
very simple rational processes for computing the cube root of 2, so we can
realize that ancient mathematicians had at hand the most elemental arithmetic
tools for solving problems related to what we call nowadays algebraic equations
of any degree.
![]()
Rational
process (RP-1) for approximating: cube root of 2
(Note: In
this web page the Spanish acronym: Mr must be interpreted
as: Rational Mean (Rm)
Given the initial set of
three values:
![]()
whose product is trivial
and equal to 2. According to our notation for the rational mean, the rational process for approximating the
cube root of 2 is as follows:
![]()
![]()
![]()
![]()
![]()
![]()
and so on...
At each stage, we get a set
of three approximations (whose product is trivial and equal to 2) by defect and
excess to the cube root. It is necessary to remark that in order to develop
this natural rational process we need: No decimals, No trial-&-error method
and No Cartesian system.
We can also express the
above rational process in the following way:
Given the initial set:
![]()
the rational process to the
cube root of P is:
![]()
![]()
Another
rational process (RP-2), related to the well known Daniel Bernoulli's
method
Given the
initial set:
![]()
The new rational process to
the cube root of P is:
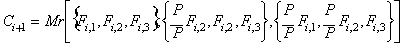
which converges slightly
faster than the previous one, both of them being directly related to
Bernoulli's method and Generalized continued fractions.
![]()
Accelerated
rational process ARP-2a
Given the
initial set:
![]()
By computing the following
rational means equivalent to the harmonic and arithmetic means:
![]()
180/143 corresponds to the harmonic mean and 227/180 to the arithmetic mean. It is easy to find a third value v3,
so: (180/143)*(227/180)*(v3) = 2, thus, v3 =
(2*143)/227 = 286/227. The new set of three rational approximations is:
![]()
The value 286/227 is also a
rational mean between the initial three
fractions, however, assuming we are ancient mathematicians I prefer to disclose
the method in this very simple way. By repeating the above steps and picking up
just the third approximation of each new set, we get the following table of
values which includes a comparison with Newton's method:
|
|
|||
|
Accelerated
Rational Process
(ARP-2a) |
Newton's
Method |
||
|
Approximations:
xi |
Error |
Approximations: xi |
Error |
|
286 |
9E-6 |
63 |
8E-5 |
|
27825466 |
2E-12 |
375047 |
-5E-9 |
|
25649277607024348370746 |
7E-26 |
158262616209301396 |
-2E-16 |
Rational Process ARP-2b
Given the
initial set:
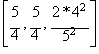
By computing the following
rational means equivalent to the harmonic and arithmetic means:
![]()
It is fairly easy to check
that a third value v3, so: (160/127)*(63/50)*(v3)=2,
is v3 = (2*127*50)/(160*63) = 635/504.
![]()
(The value 635/504 is also
a rational mean between the initial three
fractions.)
By evaluating three steps
and picking up just the third approximation of each new set, we get the
following errors: 4 E-7, 3 E-20, 1 E-59, that is, 59 exact digits in the third
step.
![]()
Trivial formulation of Newton's and
Halley's methods by means of the
Rational Process
Square
root of P, Newton's method and the rational process
Given the
initial set:
![]()
whose product is trivial
and equal to P. Making their denominators the same and computing the
rational mean (Ar=Arithmetic mean):
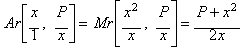
We get a mean value between
the initial two fractions, a closer approximation to the square root of P,
in other words, an iteration function equivalent to Newton's method when
applied to x2-P.
![]()
Square
root of P, Halley's method and the rational process
Given the
initial set:
![]()
whose product is trivial
and equal to P2, that is, four approximations to the square
root of P.
![]()
By computing the Arithmonic mean of the third degree (ATM3)
between those initial values:
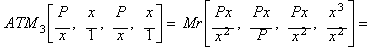
![]()
we get a mean value between
the initial four fractions, a closer approximation to the square root of P,
in other words, an iteration function equivalent to Halley's method when
applied to x2 - P.
![]()
Cube
root of P, Newton's method and the rational process
By
computing the arithmetic mean (Ar):
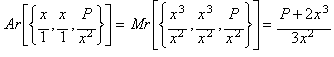
we get an iteration
function corresponding to Newton's method when applied to: x3 -
P.
![]()
Cube
root of P, Halley's method and the rational process
By
computing the arithmonic mean of the second degree (ATM2):
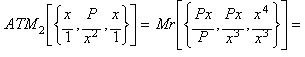
![]()
we get an iteration
function equivalent to Halley's method when applied to: x3- P.
![]()
Fourth
root, Newton's method and the rational process
Given the
initial set:
![]()
of four approximations to
the fourth root of P.
Then by computing the arithmetic mean (Ar):
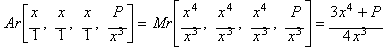
we get an iteration
function equivalent to Newton's method when applied to x4 - P.
![]()
Fourth
root, Halley's method and the rational process
Given the
set:
![]()
whose product is trivial
and equal to P2, eight approximations to the fourth root of P.
![]()
By computing the arithmonic mean of the fifth order ATM5 :
![]()
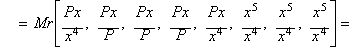
![]()
we get an iteration
function equivalent to Halley's method when applied to: x4-
P.
![]()
Fifth
root, Newton's method and the rational process
Given the
initial set:
![]()
The arithmetic mean yields:
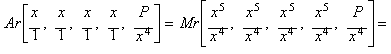
![]()
the iteration function equivalent
to Newton's method when applied to x5 - P.
![]()
Fifth
root, Halley's method and the rational process
Given the
set:
![]()
The Arithmonic mean of the third order ATM3
yields:
![]()
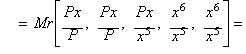
![]()
an iteration function
equivalent to Halley's method when applied to x5 - P.
![]()
Halley's
method general expression
From all
the previous sections it is easy to formulate the general expression for
Halley's method:
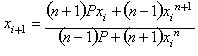
for solving the n-th
root of P.
![]()
New
iteration functions
By using
other initial sets it is easy to find a new iteration function (IF-1)
for solving the n-th root of P:
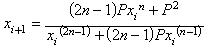
which also triples the
number of exact digits in each iteration.
You can also find another
iteration function (IF-2), i.e.: specifically for the square root of P:
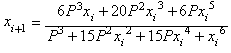
(It could be of some interest
to the reader to find the general expression for the n-th root of P )
In the case of the square
root of 2, let's evaluate the errors for the above two new methods and
Halley's.
|
|
|||
|
|
FI-1 |
FI-2 |
Halley's |
|
i |
Errors |
||
|
1 |
0.014357 |
-7.21 E-5 |
0.014214 |
|
2 |
3.64 E-7 |
-7.79 E-28 |
3.64 E-7 |
|
3 |
6.05 E-21 |
-1.24 E-165 |
6.05 E-21 |
|
4 |
2.77 E-62 |
-1.98 E-992 |
2.77 E-62 |
![]()
CONCLUSIONS
Based on
the extremely simple arithmetical processes and wonderful properties of Number
shown above and considering the incomprehensible absence of any precedent on
this matter all through the history of Arithmetic and roots solving, one can
see now that it is certainly a ridiculous arrogance to think that the
artificial creations (i.e.: cartesian system, decimal fractions, imaginary
numbers, etc.) of any individual could ever exceed the natural order determined
by God in accordance with the harmonies of Number.
![]()
Copyright ©
1993-2002
All rights reserved under international
Copyright Conventions.
No part of this page may be reproduced, stored or transmitted in any
form or by any means
without the prior permission
of the author: D. Gómez.
Last revision: 2002