|
.
|
Generalized
continued fractions
A new general concept on
continued fractions extracted from the book: “LA QUINTA OPERACIÓN ARITMÉTICA, Revolución del Número” (Title
translation: The Fifth Arithmetical Operation, Number Revolution) ISBN:
980-07-6632-4. Copyright ©. All rights reserved under international Copyright
Conventions. Author: D. Gómez.
![]()
CONTENTS:
![]()
Generalized Continued Fractions
Fractal Fractions
Given the algebraic
equation f(x) = 0 of n-th degree:
![]()
Its maximum modulus root
can be expressed in terms of a generalized continued fraction (Fractal
Fraction), as follows:
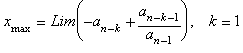
By replacing the fractional
part at each stage by the expression:
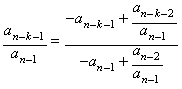
all this yields the
following general expression for the maximum modulus root of f(x):
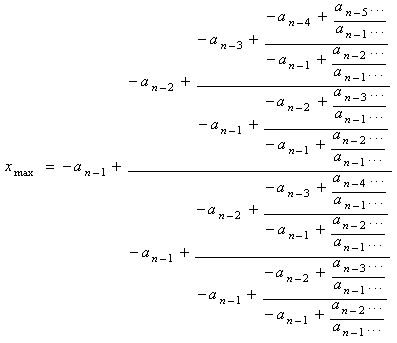
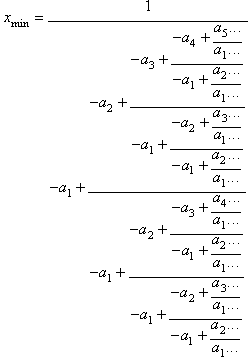
The minimum modulus root of
the equation:
![]()
is given by the following
generalized continued fraction:
![]()
Example:
Being a0
= -1, a1 = -2, the representation of the maximum modulus root
of the equation:
![]() as a
generalized continued fraction is:
as a
generalized continued fraction is:
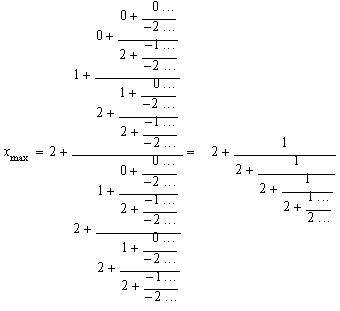
We can see that the
traditional continued fraction expression of the irrational:
![]() is
just a second order expression of the new generalized continued fraction
concept.
is
just a second order expression of the new generalized continued fraction
concept.
It is necessary to redefine
the representation of irrational numbers by means of traditional continued
fractions.
![]()
Another example:
Given the
equation (x+1)3 =2, or the same -x3-3x2-3x+1=0,
whose minimum modulus root is
![]() .
Thus, being a1 = -3, a2 = -3, a3
= -1, the generalized continued fraction expression for this root is:
.
Thus, being a1 = -3, a2 = -3, a3
= -1, the generalized continued fraction expression for this root is:
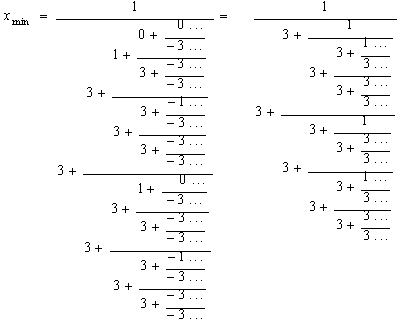
A very interesting
expression bringing a periodical representation of a cubic irrational.
The convergents of this
fractal fraction are:
![]()
yielding successive
approximations to
![]() .
.
This sequence of convergents
is ruled by the following lineal homogeneous recurrence relation:
yn=3yn-1 + 3yn-2
+ yn-3
It is important to notice
that even the generalized continued fractions are just a special case of the
Rational Process (Based on the rational mean).
If one try to represent the
cube root of 2 by means of the traditional continued fractions (Second order
continued fractions as we should call them) then we'll get a distorted representation
(non-periodic coefficients) of this irrational number, as follows:
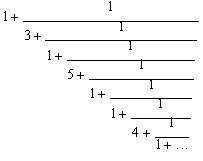
whose convergents are:
![]()
![]()
Conclusions
It is clear
that traditional continued fractions should be better called: “Second Order Continued
Fractions”. As we have seen in the above numerical examples, when trying to
represent a cubic irrational by means of a second order continued fraction
(traditional concept) then one get a disfigured image of the irrational. It is
necessary to redefine the traditional representation of irrational numbers by
means of continued fractions.
Generalized Continued
Fractions (Fractal Fractions) are directly related to the Rational Process (Rational Mean)
![]()
Copyright ©
1993-2002
All rights reserved under international
Copyright Conventions.
No part of this page may be reproduced, stored
or transmitted in any form or by any means
without the prior permission of the author: D. Gómez.
Last revision: 2002