|
|
Rational
Mean: (Generalized Mediant)
Brief definition, some
examples and observations extracted from the book: “LA QUINTA
OPERACIÓN ARITMÉTICA, Revolución del Número” (Title translation: The Fifth Arithmetical Operation,
Number Revolution) ISBN: 980-07-6632-4. Copyright ©. All rights reserved under
international Copyright Conventions. Author: D. Gómez.
CONTENTS:
![]()
The Rational Mean
(Generalized Mediant)
Rational
Mean Definition
Given any
set V of n positive rational numbers arranged according to their
magnitudes:
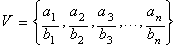
The expression:
![]()
is a mean value (Rational
Mean, Rm) between the extreme values (a1/b1),
(an/bn):
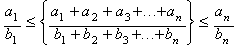
A more general notation for
multiple rational means can be expressed this way:
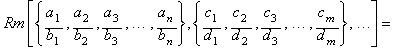
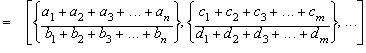
Example:
![]()
The following case:
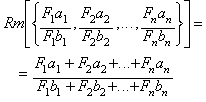
is also the rational mean
between the same n rational numbers, this time by modifying the form of
each fraction using the factors: F1, F2,...,
Fn.
We can say that given any
set of n values taken at will (integers, rational or irrational)
arranged in an increasing order:
![]()
and given another set [F1,
F2, F3, . . ., Fn] of any positive
values (integers, rational or irrational), then the expression:
![]()
is the rational mean
between the values v1,v2,v3,
... ,vn
![]()
General
Rational Operation (Gro) Definition:
We can go
further by defining the (Gro) General Rational Operation (not
necessarily a mean value) between n arbitrary values v1,v2,v3,
... ,vn as stated in the following example: Given n values
v1=a1, v2=(-a2/b2),
v3=(a3/b3), v4=-a4,
. . . , v5=-an , the Gro
between those values is:
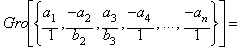
![]()
Moreover, Given n
rational functions: f1(x)/g1(x),
f2(x)/g2(x), f3(x)/g3(x),
..., fn(x)/gn(x), the General
Rational Operation (not necessarily a mean value) is:
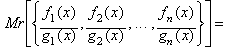
![]()
as said, not necessarily a
mean value. In some cases the General Rational Operation becomes a Rational
Mean between those n rational functions.
Any algorithm based on the
Rational Mean will be called: Rational Process.
The analysis of the
rational mean (Rm) has been restricted –all through the history of
mathematics– to the specific case called Mediant (n=2) and some curious
properties of Farey series, Ford's circles, Stern-Brocot tree and the
generation of the convergents of the simple continued fractions:
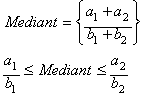
![]()
Comments
Some
experts usually state that this operation is not well defined within the set of
rational numbers, that is, the rational mean works with ordered pairs of
numbers. As an example, let's compute the rational mean (mediant):
Rm[3/2, 4/3]= 7/5
and the rational mean
between the same values this time using 6/4 instead of 3/2:
Rm[6/4, 4/3]= 10/7
Same values, same
operation, however, different results.
Now, if we argue that this
operation is not “well defined“ within the set of rational numbers, then we
must also say that the following mathematical operations are not well defined,
mainly when considering that the rational mean is the fundamental principle
which rules them:
•The Harmonic mean: Rational mean between fractions having equal
numerators.
•The Arithmetic mean: Rational mean between fractions having equal
denominators.
•The Arithmonic mean: Rational mean between fractions having some
of their denominators and numerators the same, according to an specific rule.
•Generation of convergents
of generalized continued fractions.
•Algebraic and
transcendental numbers.
•Bernoulli's, Newton's, Halley's methods for solving algebraic equations.
•Power series expansions
(Maclaurin-Taylor series).
•Definition of the
arithmetical operations of irrational numbers.
•Statistics.
•Gravity center.
•Ford's circles
•Farey's fractions
Contrary to the mainstream of
thought of many modern mathematicians, it is clear that the issue on the
"definition" of this operation within the set of rational numbers
should be considered from a very different point of view, I mean, a new vision
which clearly differs from the cartesian system principles.
As said, contrary to the
Cartesian system fundamentals, Number should not be considered just as an
"absolute" value (the term "absolute" means "decimal
value"). In the same way flowers bring us their multiple natural properties:
beauty, color and scent, also Number bring out much more than just an absolute
value: It bears a relative value (The form of the ratio) and a very specific
location within a set of ratios which plays an important role in the
development of roots solving algorithms. The relevance of all these properties
of Number will become evident to the reader mainly when using the new Arithmonic Mean. Cartesian system have depersonalized Number
confining it to just an absolute value (decimal value).
Indeed, it is really
striking to realize that ancient mathematicians (Babylonians, Greeks, etc.)
certainly had at hand the most elemental arithmetic tool (The rational mean)
for achieving all those "advanced" algorithms that has been
consecrated as the most outstanding successes brought to light by the Cartesian
system and decimal fractions. Believe It or Not!, based on all the evidences,
it seems that the extremely simple arithmetic methods shown in the book “The
Fifth Arithmetic Operation” have no precedents at all, all through the very
long story on roots solving.
Based on the new elemental
rational processes and many other considerations you will realize that:
•The Cartesian system
cannot be considered as a fundamental system of Natural Philosophy but just as
an artificial creation which apart from being extrinsic to the natural
properties of Number also contributes to distort and vitiate the genuine image
of Quantity. Contrary to the mainstream of the Cartesian system, Number should
not be considered just as an "absolute" value (the term
"absolute" means "decimal value" commonly used in Cartesian
system). In the same way a flower bring us its multiple natural properties:
beauty, color and scent, also Number bring outs much more than just an absolute
value: It bears a relative value (The form of the ratio) and a very specific
location within a set of ratios. The importance of all these properties of
Number will become evident to the reader mainly when using the new Arithmonic Mean.
•The arithmetical
operations of irrational numbers can be easily defined by agency of the
Rational Process (based on the Rational Mean in accordance with Number, not by
any other but Number itself), rather than by using Dedekind's and Cantor's
opinions and judgments.
•The traditional continued
fractions expressions are just a particular case (Second Order Continued
Fractions) of a more general conception called: “Generalized Continued Fractions” (Fractal Fractions), which yield
periodic representations for algebraic numbers of higher degrees. You will
realize that any representation of irrational numbers of higher degrees get
distorted when using the traditional continued fractions, that is, the “Second
Order Continued Fractions”
•Surprisingly, there are
few precedents on the analysis of the rational mean, most of them on the
special case: Mediant. Some people who worked with this operation: Nicolas
Chuquet (1484), Haros(1802), Farey(1816), Cauchy, J. Wallis, C. S. Peirce,
Stern-Brocot(1858-1860), D. Hidalgo (1963). Lester R. Ford's circles and Pick's
theorem are also related to this operation.
•The rational mean is the
most elemental arithmetical operation for roots solving, it also rules the power series expansions and
the generation of transcendental numbers.
•The Arithmonic Mean is an essential and very simple operation
which --from all the evidences--have been passed over all through the whole
history of mathematics.
•Based on all those important
arithmetical methods, number properties and observations that have been passed
over during so long time, one can say now that it is certainly a pathetic
arrogance to think that any result (i.e.: imaginary numbers, higher dimensions,
cartesian system, relativity theory, etc.) coming out of the opinions and
judgments of any mathematician, could ever supersede the natural order and
wonderful properties determined “in accordance with number by the forethought
and the mind of Him that created all things, for the pattern was fixed, like a
preliminary sketch,...” (quoted text: Nicomachus, chap.VI, [1]).
![]()
Copyright ©
1993-2002
All rights reserved under international
Copyright Conventions.
No part of this page may be reproduced, stored or transmitted in any
form or by any means
without the prior permission
of its author: D. Gómez
Last revision: 2002